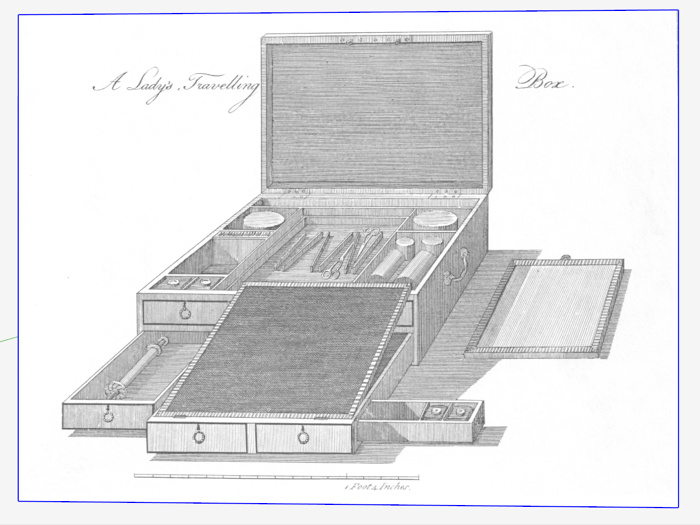
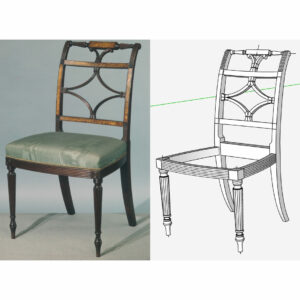
At this week’s conference “Working Wood in the 18th Century” in Colonial Williamsburg, I was intrigued by Brian Weldy’s presentation on Thomas Sheraton’s drawing representations of the Lady’s Travelling Box. It was necessary for Brian, and Mack Headley (master cabinetmaker), to dissect Sheraton’s drawing to create their own version of this box.
Brian showed Sheraton’s drawing as depicted in his book “The Cabinetmaker and Upholsterers Drawing Book”. He also illustrated , with pencil, drawing board, T-square, and compass, how to decompose the strange drawing format, into critical dimensions necessary for the construction.
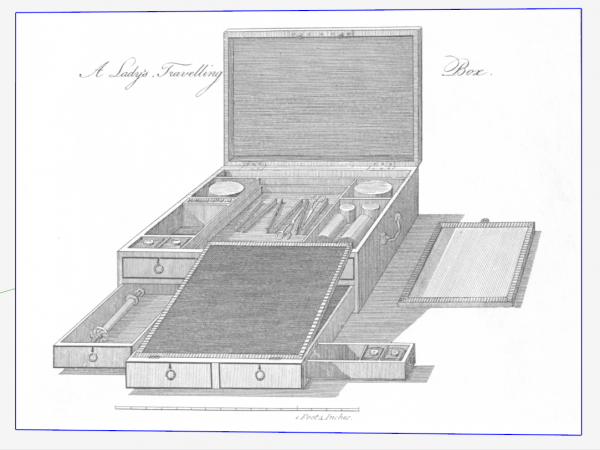
I suppose the engineering background drives my interest in this strange perspective drawing representation, and how one could discover dimensional information necessary for building the box.
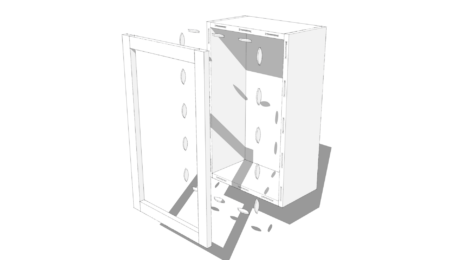
I fired up SketchUp on my first day back home and imported the Sheraton drawing shown above.
Since this is not a photo rather a corruption of a perspective sketch, I suspected that SketchUp’s Photo Match capability would not be much help. I tried anyway, and indeed found out quickly that it wouldn’t produce acceptable results. It’s as if Sheraton decided to make the front face of the box in Orthographic View, and then draw out the rest of the box in single point perspective. That’s quite a combination within one sketch.
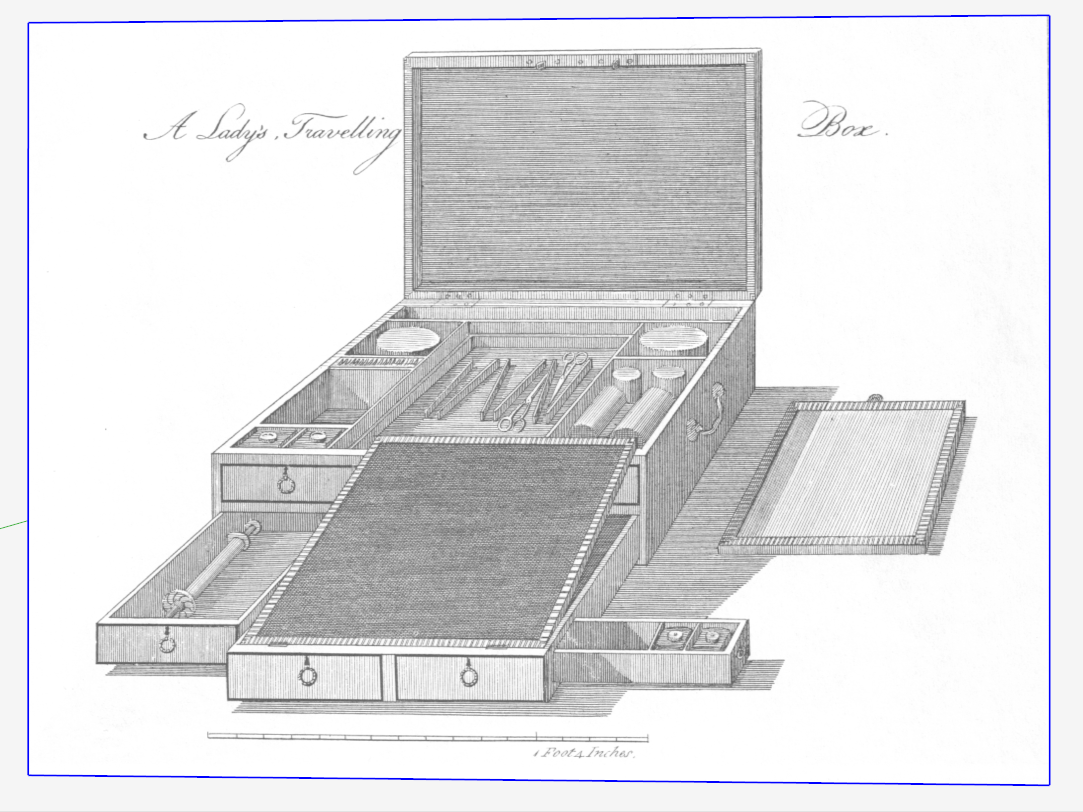
Sheraton provides a scale on his sketch, so this is very helpful in determining component dimensions. Since the front face of the box is straight-on in view, it’s easy to discover the width and height of the box. The trick is determining the depth of the box.
The key to this unknown is the fact that the top of the box is perpendicular and also facing the front. Its dimensions are reduced due to the top being located at the back edge of the box. The open top’s height is proportional to the actual real depth of the box. To find it’s real height I used the vanishing point and guidelines to project the height at the front location as it intersects the picture frame.

See the following video of this process of determining key overall box dimensions.
Note that I did not use 3D at all in this exercise – only 2D – that’s extremely rare for me.



















Comments
I haven't even started in on all that you are presenting here but I am already getting an inkling of things to come in your presentation.
GREAT STUFF !
This is what I come to FWW for, or used to, dang this is enough to make me resubscribe/reup my membership .
Thank You !
Thank you Tim for a nice SketchUp exercise! But for those of us who are not so familiar with SketchUp, there is a simpler way to calculate the dimensions of the traveling box. Since both the front and the back of the box are shown in isometric/orthographic projection, you have the true proportions of both the front of the box and its depth (the hight of the lifted top). As it turns out, the front's proportions are 1 to 4, and dividing 15 3/4" by 4 will give you a dimension of 3.9375, or 3 15/16", just as you have calculated. Ditto for the box's depth: the proportions of the box cover are 1 to 1 to 1.5. Dividing 15 3/4" by 1.5 will produce a dimension of 10.227, or approximately 10 1/4". If you check the proportions on the original drawing you will be able to verify that dimension. So, I am afraid that your SketchUp calculation using the perspective -- a not so accurate method in any case -- overestimated the depth of the box by 9/16". Not a major differense, but if you compare the proportions of the top of the box and your suggested rectangle, you will see that they are not exactly the same.
Enjoy the construction of the box!
To Polimantilas: you are correct and the ratio method is valid and works. There are numerous errors in using any of these methods in scanning, copying, straightening, measuring, and drawing coincident lines. It is probably A good idea to work it out multiple ways and compare with other pieces.
Tim
Polymantilas: I think you should check your division. I don't get the same results as you, but replicate the values determined by SketchUp.
12.75/9=1.412
15.75/1.412=11.15
These are the values that are very close to those calculated in Williamsburg. They ended up at 15.875 width and 11.18 length.
Tim
Log in or create an account to post a comment.
Sign up Log in